백준 1504(특정한 최단 경로) - Python(파이썬) - 최단 경로
반응형
참고자료 : 다익스트라 알고리즘 참고 자료
[이코테] CHAPTER 09 최단 경로 알고리즘 - 다익스트라 최단 경로 알고리즘
최단 경로 알고리즘(Shortest Path) : 가장 짧은 경로를 찾는 알고리즘 1) 최단 경로 문제- 지점( 노드 ), 지점 간 연결된 도로( 간선 ) - 한 지점에서 다른 한 지점까지의 최단 경로를 구해야 하는 경우
coooco.tistory.com
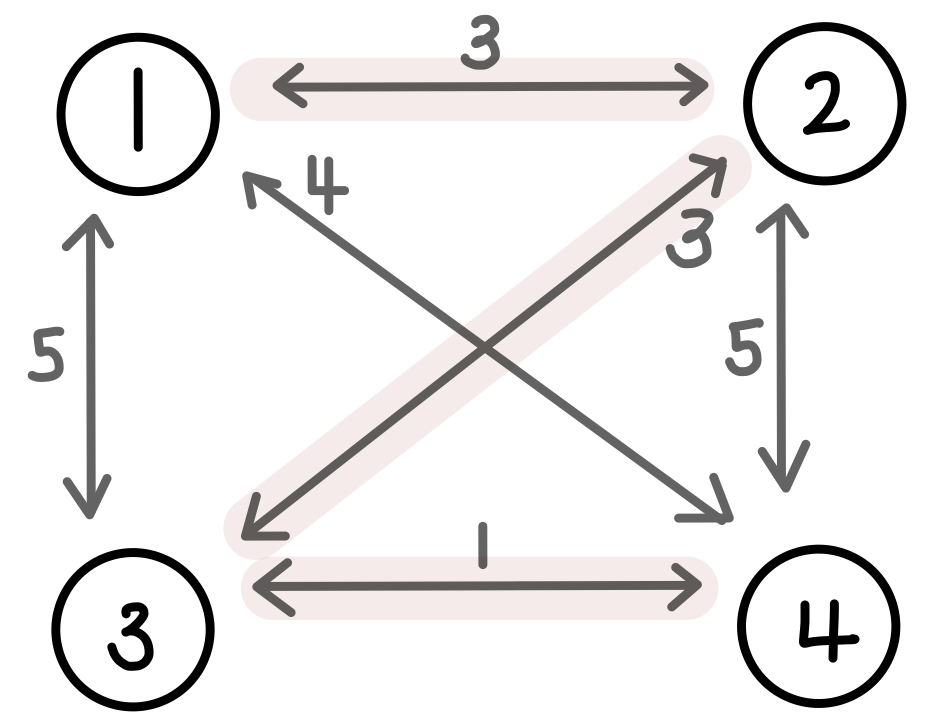
예제 설명

| 1번 노드에서 시작할 경우 | ||||
| 도착 노드 | 1번 | 2번 | 3번 | 4번 |
| 최소 비용 | 0 | 3 | 5 | 4 |
| 2번 노드에서 시작할 경우 | ||||
| 도착 노드 | 1번 | 2번 | 3번 | 4번 |
| 최소 비용 | 3 | 0 | 3 | 4 |
| 3번 노드에서 시작할 경우 | ||||
| 도착 노드 | 1번 | 2번 | 3번 | 4번 |
| 최소 비용 | 5 | 3 | 0 | 1 |
1번 노드 -> 2번 노드 -> 3번 노드 -> 4번노드 인경우 최단 거리 : 3 + 3 + 1 = 7
1번 노드 -> 3번 노드 -> 2번 노드 -> 4번노드 인경우 최단 거리 : 5 + 3 + 4 = 12
즉, 2번노드와 3번 노드를 지날 때 최단 거리는 7이다.
다익스트라 알고리즘은 한 지점에서 다른 특정 지점까지의 최단 경로를 구해야하는 경우에 사용하는 알고리즘이다.
처음 노드 : 1번 | 끝나는 노드 : n번
- d1 = dijkstra(1) : 1번 노드에서 시작했을 경우 다익스트라 알고리즘을 이용해 만든 최단 거리 테이블
- dv1 = dijkstra(v1) : v1번 노드에서 시작했을 경우 다익스트라 알고리즘을 이용해 만든 최단 거리 테이블
- dv2 = dijkstar(v2): v2번 노드에서 시작했을 경우 다익스트라 알고리즘을 이용해 만든 최단 거리 테이블
1번 -> v1 -> v2 -> n번 : d1[v1] + dv1[v2] + dv2[n]
1번 -> v2 -> v1 -> n번 : d1[1] + dv2[v1] + dv1[n]
이런식으로 구해서 비교하여서 최단 거리 테이블을 구한다.
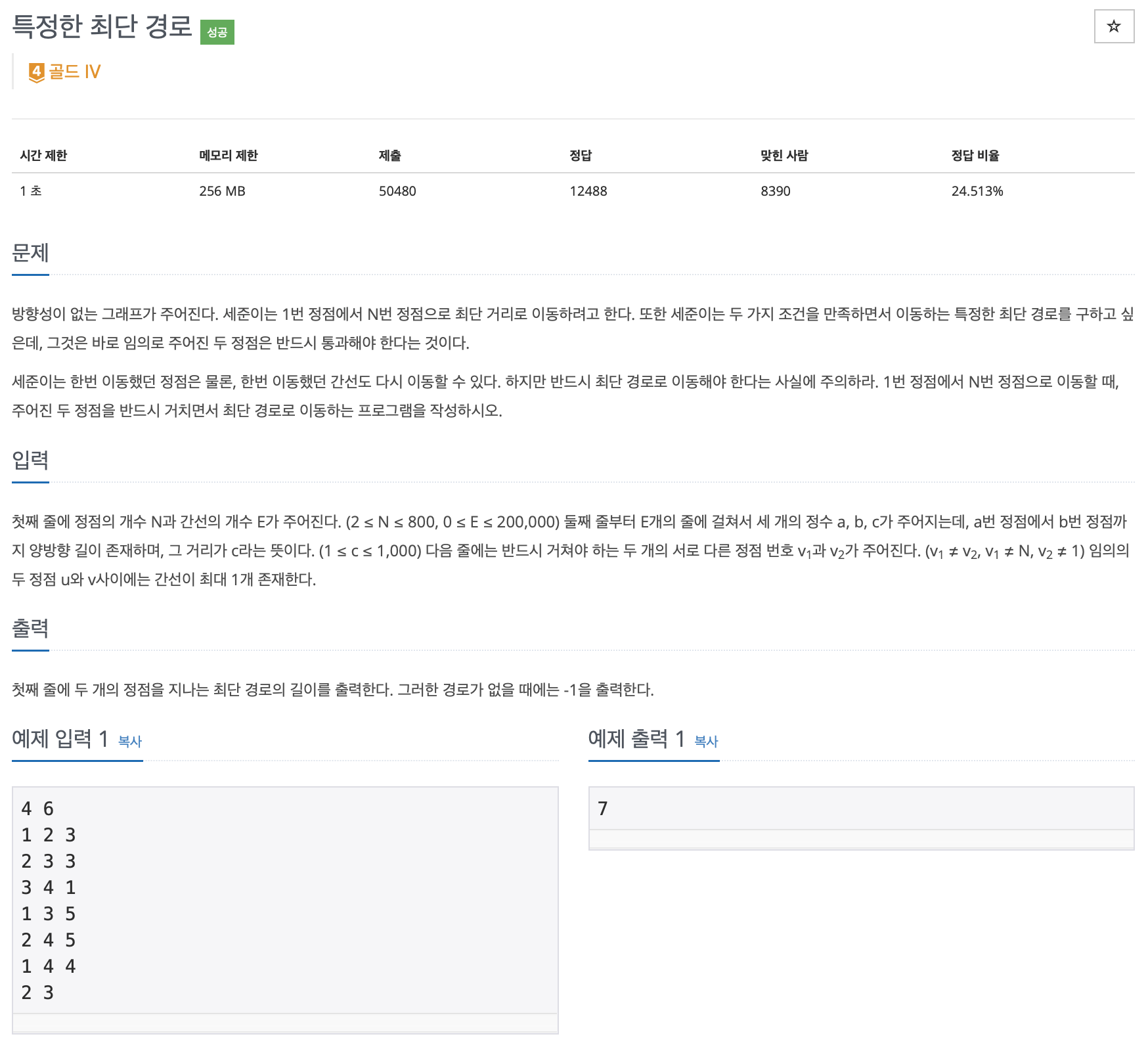
문제 설명
① 다익스트라 알고리즘 함수(dijkstra(시작노드)) 만들어 최단 거리테이블 반환하기
② 함수를 사용하여 1번노드에서 시작한 최단 거리테이블(d1), v1에서 시작한 최단 거리테이블(dv1), v2에서 시작한 최단 거리테이블(dv2)을 만들기
③ (d1[v1] + dv1[v2] + dv2[n])와 (d1[1] + dv2[v1] + dv1[n]) 둘 중 최솟값을 출력하지만 만약 무한대를 넘을 경우 -1을 출력
코드 작성
💻Python(파이썬)
import sys
import heapq
#정점의 개수, 간선의 개수
n,e = map(int,sys.stdin.readline().split())
INF = int(1e9)
#간선끼리 연결된 그래프
graph=[[] for _ in range(n+1)]
#간선끼리의 연결 그래프
for i in range(e):
a,b,c = map(int,sys.stdin.readline().split())
graph[a].append((b,c))
graph[b].append((a,c))
#다익스트라 함수 구현
def dijkstra(start):
distance = [INF]*(n+1)
distance[start]=0
q =[]
heapq.heappush(q,(0,start))
while q:
dist,now = heapq.heappop(q)
if distance[now]<dist:
continue
for i in graph[now]:
cost = dist + i[1]
if cost<distance[i[0]]:
distance[i[0]]=cost
heapq.heappush(q,(cost,i[0]))
return distance
#꼭지나야하는 점 v1,v2 받기
v1,v2 = map(int,sys.stdin.readline().split())
d1=dijkstra(1)
dv1=dijkstra(v1)
dv2=dijkstra(v2)
dv3 = dijkstra(4)
#n -> v1 -> v2 -> k
#n -> v2 -> v1 -> k
result = min(d1[v1]+dv1[v2]+dv2[n],d1[v2]+dv2[v1]+dv1[n])
print(result if result<INF else -1)
반응형
'[백준] Python,Java로 풀기📖 > 최단거리' 카테고리의 다른 글
| 백준 4485(녹색 옷 입은 애가 젤다지?) - 다익스트라알고리즘, 힙구조, 최단거리- python (0) | 2024.11.04 |
|---|---|
| 백준 10159(저울) - Python(파이썬),Java(자바) - 플로이드 워셜 (0) | 2022.06.26 |
| 백준 1140(플로이드) -Python(파이썬) - 플로이드워셜 알고리즘 (0) | 2022.06.20 |
| 백준 2110(공유기 설치) - Python(파이썬) - 이분탐색 (0) | 2022.06.20 |
댓글
이 글 공유하기
다른 글
-
백준 4485(녹색 옷 입은 애가 젤다지?) - 다익스트라알고리즘, 힙구조, 최단거리- python
백준 4485(녹색 옷 입은 애가 젤다지?) - 다익스트라알고리즘, 힙구조, 최단거리- python
2024.11.04 -
백준 10159(저울) - Python(파이썬),Java(자바) - 플로이드 워셜
백준 10159(저울) - Python(파이썬),Java(자바) - 플로이드 워셜
2022.06.26 -
백준 1140(플로이드) -Python(파이썬) - 플로이드워셜 알고리즘
백준 1140(플로이드) -Python(파이썬) - 플로이드워셜 알고리즘
2022.06.20 -
백준 2110(공유기 설치) - Python(파이썬) - 이분탐색
백준 2110(공유기 설치) - Python(파이썬) - 이분탐색
2022.06.20