[이코테] CHAPTER 09 최단 경로 알고리즘 - 다익스트라 최단 경로 알고리즘
최단 경로 알고리즘(Shortest Path) : 가장 짧은 경로를 찾는 알고리즘
1) 최단 경로 문제- 지점( 노드 ), 지점 간 연결된 도로( 간선 )
- 한 지점에서 다른 한 지점까지의 최단 경로를 구해야 하는 경우
- 한 지점에서 다른 모든 지점까지의 최단 경로를 구해야 하는 경우
- 모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우
2) 최단 경로 알고리즘 종류 - 다익스트라 최단 경로 알고리즘 , 플로이드 워셜
1. 다익스트라(Dijkstra) 최단 경로 알고리즘
: 특정한 한 노드에서 출발하여 다른 노드로 가는 각각의 최단 경로를 구해주는 알고리즘
- 음의 간선(0보다 작은 값을 가지는 간선)이 없을 때 정상적으로 동작 -> GPS 소프트웨어(길찾기)의 기본 알고리즘 채택
- 그리디 알고리즘으로 분류 -> 매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정을 반복
- 동작과정
① 출발 노드를 설정 ( 하나의 출발 노드로부터 시작하므로 )
② 최단 거리 테이블을 초기화 ( 모든 노드까지 가는 것을 무한으로 설정, 자기 자신에서 자신으로 가는 노드만 0으로 설정)
③ 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택
④ 해당 노드를 서쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신
⑤ 3번, 4번 반복


힙 자료구조를 사용한 다익스트라 알고리즘 ( 시간복잡도 O(ElogV) : E(간선의 개수), V(노드의 개수) )
- 힙 자료구조는 우선순위 큐(우선순위가 가장 높은 데이터를 가장 먼저 삭제)를 구현하기 위하여 사용하는 자료구조 중 하나
- 파이썬 : ProiorityQueue 혹은 heapq를 사용
( 일반적으로 heapq가 더 빠르게 동작하므로 수행 시간이 제한된 상황에서는 heapq 사용 권장 )
- 우선순위 큐를 구현 할 때는 최소 힙(Min Heap), 최대 힙(Max Heap) 을 이용
최소 힙 : 값이 낮은 데이터가 먼저 삭제, 최대 힙 : 값이 큰 데이터가 먼저 삭제
파이썬 : 최소 힙 구조, 자바 : 최소 힙 구조 , C++: 최대 힙 구조 이용
- 힙 자료구조를 이용하는 다익스트라 알고리즘의 시간 복잡도 : O(ElogV)
-> 노드를 하나씩 꺼내 검사하는 반복문(while)문은 최대 간선의 개수 (E)만큼 연산이 수행될 수 있다
-> E개의 원소를 우선순위 큐에 넣었다가 모두 빼내는 연산과 매우 유사(O(ElogE))
-> O(ElogE)의 E는 V^2보다 작을 것이기에 O(ElogV^2)으로 표현할 수 있고
로그의 기본 공식에 따라서 O(2ElogV)로 표현 가능 -> 빅오 표기법상 2는 제거되어서 O(ElogV)라고 볼 수 있다.
파이썬 힙 라이브러리 사용 예제
1) 최소 힙 구조
import heapq
#오름차순 힙 정렬 (Heap Sort)
def heapsort(iterable):
h=[]
result=[]
#모든 원소를 차례대로 힙에 삽입
for value in iterable:
heapq.heappush(h,value) #데이터 넣을 떄
#힙에 삽입된 모든 원소를 차례대로 꺼내어 담기
for i in range(len(h)):
result.append(heapq.heappop(h))#데이터를 꺼낼 때(heappop)
return result
result = heapsort([1,3,5,6,9,2,4,6,8,0])
#최소 힙 방식으로 정렬되므로 오름차순 정렬으로 나옴
print(result)#[0,1,2,3,4,5,6,7,8,9]
2) 최대 힙 구조
파이썬에서는 별도로 최대 힙 구조를 제공하지 않으므로 최대 힙을 이용하고 싶을 경우에는 힙에 넣을 때 데이터의 부호를 바꿔서 넣은 뒤에 꺼낼 때 데이터의 부호를 바꾸어서 꺼낸다.
import heapq
#내림순 힙 정렬 (Heap Sort)
def heapsort(iterable):
h=[]
result=[]
#모든 원소를 차례대로 힙에 삽입
for value in iterable:
heapq.heappush(h,-value) #데이터 넣을 때 부호를 바꾸어서 넣기
#힙에 삽입된 모든 원소를 차례대로 꺼내어 담기
for i in range(len(h)):
result.append(-heapq.heappop(h))#데이터를 꺼낼 때도 부호를 바꾸어서 꺼내기
return result
result = heapsort([1,3,5,6,9,2,4,6,8,0])
#최소 힙 방식으로 정렬되므로 오름차순 정렬으로 나옴
print(result)#[0,1,2,3,4,5,6,7,8,9]
다익스트라 알고리즘 + 힙 자료구조 사용
단계마다 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하기 위해 힙 자료구조를 사용한다.
현재 가장 가까운 노드를 저장해 놓기 위해서 힙 자료 구조를 추가적으로 이용한다.

1번 노드가 출발인 경우를 고려. 우선순위 큐에는 (거리 0: 노드 1) 의 정보를 가진 객체 저장

우선순위 큐에서 (거리 0. 노드 1)의 정보를 꺼낸뒤 1번 노드를 거쳐서 2번,3번,4번 노드로 가는 최소 비용을 계산
차례대로 2(0+5) , 5(0+5),1(0+1) 이다. 더 짧은 경로를 찾은 노드 정보들은 우선 순위 큐에 저장하므로 세정보 모두 저장

우선순위 큐에서 (거리 1: 노드 4)의 정보를 꺼낸 뒤 4번 노드를 거쳐서 3번,5번 노드로 가는 최소 비용을 계산
차례대로 4(1+3) , 2(1+1)이다. 더 짧은 경로를 찾은 노드 정보들은 우선 순위 큐에 저장하므로 두정보 모두 저장

우선순위 큐에서 (거리2: 노드2)의 정보를 꺼낸 뒤 2번 노드를 거쳐서 4번,3번 노드로 가는 최소 비용을 계산
차례대로 5(2+3), 4(2+2) 가 나오게 되는데 최단 거리를 짧게 갱신할 수 없다. 따라서 우선 순위 큐에 어떠한 원소도 저장하지 않는다.

우선순위 큐에서 (거리2: 노드5)의 정보를 꺼낸 뒤 5번 노드를 거쳐서 3번, 6번 노드로 가는 최소비용을 계산
차례대로 3(2+1),4(2+2)가 나온다.더 짧은 경로를 찾은 노드 정보들은 우선 순위 큐에 저장하므로 두정보 모두 저장

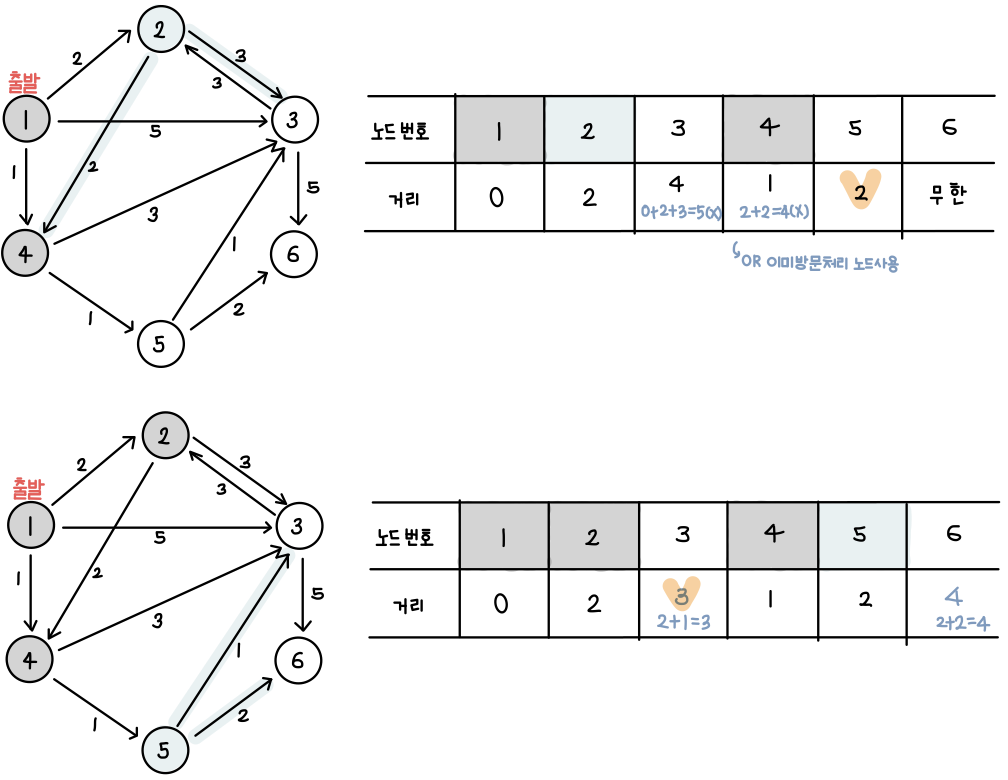
우선순위 큐에서 (거리3: 노드3)의 정보를 꺼낸 뒤 3번 노드를 거쳐서 2번, 6번노드로 가는 최소비용을 계산.
차례대로 5(3+2), 8(3+5)가 나오게 되는데 최단 거리 짧게 갱신할 수 없다. 따라서 우선 순위 큐에는 어떠한 원소도 저장하지 않는다.

우선순위 큐에서 (거리4:노드3)의 정보를 꺼낸다. 이 때, 방문한 노드 정보를 따로 담아서 표현할 수도 있지만 처음부터 표에 있는 노드번호와 비교하도록 코드를 설계하면된다. 현재 최단 거리 테이브레어서3번 노드의 최단 거리는 3과 비교하였을 때 거리4는 더 크므로 무시한다.

우선순위 큐에서 (거리4:노드6)의 정보를 꺼낸다. 이때, 노드 6은 가는 원소가 없으므로 테이블은 갱신되지 않고 우선순위 큐도 갱신되지 않는다.
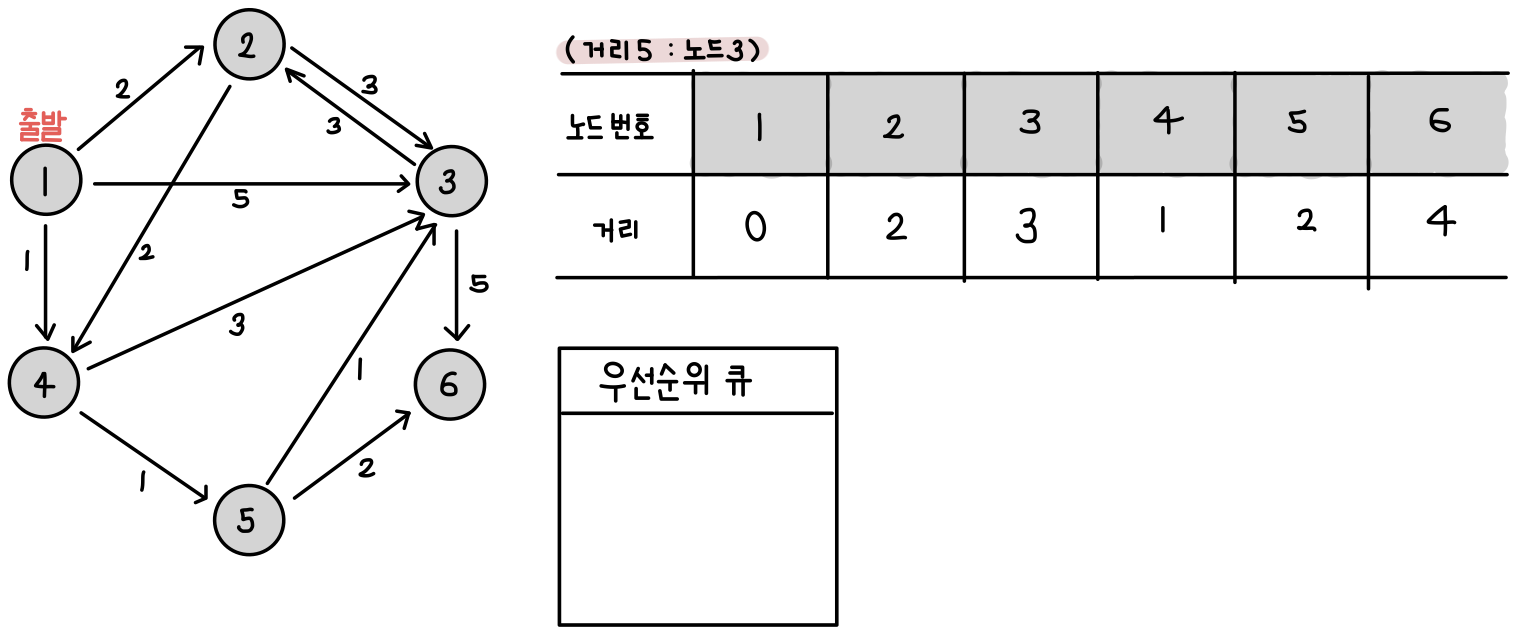
우선순위 큐에서 (거리5:노드3)의 정보를 꺼낸다. 이때, 노드 3은 최단 거리 테이블에 3이라고 하였으므로 거리5는 더 크므로 무시된다.
💻 파이썬(Python)
import heapq
import sys
input = sys.stdin.readline
INF = int(1e9)#무한을 의미하느 ㄴ값으로 10억을 설정
#노드의 개수,간선의 개수를 입력받기
n,m = map(int,sys.stdin.readline().split())
#시작 노드 번호 입력받기
start = int(sys.stdin.readline())
#각 노드에 연결되어 있는 노드에 대한 정보를 담는 리스트를 만들기
graph = [[] for i in range(n+1)]
#최단 거리 테이블을 모두 무한으로 초기화
distance = [INF]*(n+1)
#모든 간선 정보를 입력 받기
for _ in range(m):
a,b,c = map(int,sys.stdin.readline().split())
#a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph[a].append((b,c))
def dijkstra(start):
q=[]
#시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
heapq.heappush(q,(0,start))
distance[start]=0
while q:#큐가 비어있지 않다면
#가장 최단 거리와 짧은 노드에 대한 정보 꺼내기
dist,now = heapq.heappop(q)
#현재 노드가 이미 처리된 적 있는 노드라면 무시
if distance[now]<dist:#최단 거리 테이블과 거리 비교
continue
#현재 노드와 연결된 다른 인접한 노드들을 확인
for i in graph[now]:#i에는 노드,간선(거리)정보가 담겨져 있음
cost = dist+i[1]#처음 노드와 연결된 노드 정보 저장
#현재 노드를 거쳐서, 다른 노드로 이동하는 거리가 더 짧은 경우
if cost<distance[i[0]]:#테이블에 있는 연결된 노드의 정보와 비교
distance[i[0]]=cost
heapq.heappush(q,(cost,i[0]))#힙에 저장
dijkstra(start)
#모든 노드로 가기 위한 최단 거리르 출력
for i in range(1,n+1):
#도달할 수 없는 경우, 무한(INFINITY)이라고 출력
if distance[i]==INF:
print('INFINITY')
else:
print(distance[i])

자바(Java) https://github.com/ndb796/python-for-coding-test/blob/master/9/2.java
package s15_shortest;
import java.io.*;
import java.util.*;
class Node implements Comparable<Node>{
private int index;
private int distance;
public Node(int index, int distance){
this.index=index;
this.distance=distance;
}
public int getIndex() {
return this.index;
}
public int getDistance() {
return distance;
}
//거리(비용)가 짧은 것이 높은 우선순위를 가지도록 설정
@Override
public int compareTo(Node o) {
if(this.distance<o.distance){
return -1;
}
return 1;
}
}
public class s01_9_2 {
public static final int INF = (int)1e9;//무한을 의미하는 값으로 10억을 설정
//노드의 개수(N), 간선의 개수(M), 시작 노드 번호 (Strat)
//노드의 개수는 최대 100,000개라고 가정
public static int n,m,start;
//각 노드에 연결되어 잇는 노드에 대한 정보를 담은 배열
public static ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();
//최단 거리 테이블 만들기
public static int[] d = new int[100001];
public static void dijkstra(int start){
PriorityQueue<Node> pq = new PriorityQueue<>();
//시작 노드로 가기 위한 최단 경로는 0으로 설정하여, 큐에 삽입
pq.offer(new Node(start,0));
d[start]=0;
while (!pq.isEmpty()){//큐가 비어 있을 때까지 반복
//가장 최단 거리가 짧은 노드에 대한 정보 꺼내기
Node node = pq.poll();
int dist = node.getDistance();//현재 노드까지의 비용
int now = node.getIndex();//현재 노드
//현재 노드가 이미 처리된 적이 있는 노드라면 무시
if(d[now]<dist) continue;
//현재 노드와 연결된 다른 인접한 노드들을 확인
for(int i=0;i<graph.get(now).size();i++){
int cost = d[now]+graph.get(now).get(i).getDistance();
if(cost<d[graph.get(now).get(i).getIndex()]){
d[graph.get(now).get(i).getIndex()]=cost;
pq.offer(new Node(graph.get(now).get(i).getIndex(),cost));
}
}
}
}
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
start = Integer.parseInt(br.readLine());
// 그래프 초기화
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<Node>());
}
// 모든 간선 정보를 입력받기
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine()," ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
// a번 노드에서 b번 노드로 가는 비용이 c라는 의미
graph.get(a).add(new Node(b, c));
}
// 최단 거리 테이블을 모두 무한으로 초기화
Arrays.fill(d, INF);
// 다익스트라 알고리즘을 수행
dijkstra(start);
// 모든 노드로 가기 위한 최단 거리를 출력
for (int i = 1; i <= n; i++) {
// 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
if (d[i] == INF) {
System.out.println("INFINITY");
}
// 도달할 수 있는 경우 거리를 출력
else {
System.out.println(d[i]);
}
}
}
}
'Study Platform📚 > (알고리즘)- [이코테] 이것이 코딩테스트다 정리' 카테고리의 다른 글
| [이코테]CHAPTER 09 최단 경로 알고리즘 - 플로이드워셜 알고리즘 - Python(파이썬),Java(자바) (0) | 2022.06.11 |
|---|---|
| CHAPTER 6 -번외 정렬 - 위상 정렬(Topology Sort) - Python(파이썬) (0) | 2022.06.08 |
| [이코테] CHAPTER 05 DFS/BFS - BFS(deque 메서드) - Python(파이썬),Java(자바) (0) | 2022.05.18 |
| [이코테]CHAPTER 05 DFS/BFS - 스택, 큐, 재귀함수, DFS (0) | 2022.05.17 |
| [이코테] CHAPTER 06 정렬 - 계수 정렬 (0) | 2022.05.16 |
댓글
이 글 공유하기
다른 글
-
[이코테]CHAPTER 09 최단 경로 알고리즘 - 플로이드워셜 알고리즘 - Python(파이썬),Java(자바)
[이코테]CHAPTER 09 최단 경로 알고리즘 - 플로이드워셜 알고리즘 - Python(파이썬),Java(자바)
2022.06.11 -
CHAPTER 6 -번외 정렬 - 위상 정렬(Topology Sort) - Python(파이썬)
CHAPTER 6 -번외 정렬 - 위상 정렬(Topology Sort) - Python(파이썬)
2022.06.08 -
[이코테] CHAPTER 05 DFS/BFS - BFS(deque 메서드) - Python(파이썬),Java(자바)
[이코테] CHAPTER 05 DFS/BFS - BFS(deque 메서드) - Python(파이썬),Java(자바)
2022.05.18 -
[이코테]CHAPTER 05 DFS/BFS - 스택, 큐, 재귀함수, DFS
[이코테]CHAPTER 05 DFS/BFS - 스택, 큐, 재귀함수, DFS
2022.05.17